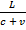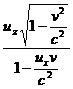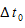TEORI RELATIVITAS KHUSUS
Relativitas merupakan salah satu
dari beberapa teori mengenai gerak yang dirancang untuk menjelaskan
penyimpangan dari mekanika Newton yang timbul akibat gerak relatif yang sangat
cepat. Teori ini yang mengubah pandangan kita mengenai ruang, waktu, massa,
energi, gerak, dan gravitasi. Teori ini terdiri atas teori khusus dan teori
umum, yang keduanya bertumpu pada dasar matematika yang kuat dan keduanya telah
diuji dengan percobaan-pecobaan dan pengamatan.
Teori
khusus, yang dikembangkan oleh Einstein pada tahun 1905, berkenaan dengan
pembanding pengukuran yang dilakukan dalam kerangka acuan inersia berbeda yang
bergerak dengan kecepatan konstan relatif satu sama lain. Di lain pihak, teori
umum yang dikemukakan tahun 1915, berkenaan dengan kerangka acuan dan gravitasi
yang dipercepat.
A.
Relativitas
Newton
Ø Semua
gerak itu relaif
Suatu
benda dikatakan bergerak bila kedudukan benda itu berubah terhadap suatu titik
acuan atau kerangka acuan. Seorang penumpang kereta api yang sedang duduk di
dalam kereta api yang bergerak meninggalkan stasiun dikatakan diam bila titik
acuannya adalah kereta api, sedangkan bila titik acuannya adalah stasiun, penumpang
tersebut dikatakan bergerak. Pengertian diam dan bergerak disini bersifat relatif tergantung titik acuannya.
Stasiun kita anggap diam, padahal stasiun bersama bumi bergerak mengelilingi
matahari, matahari bersama bumi bergerak terhadap galaksi, bintang, dan
seterusnya. Dengan demikian, dapat dikatakan bahwa tidak ada benda yang
bergerak mutlak, yang ada hanyalah gerak relatif.
Ø Definisi
kejadian, pengamat, dan kerangka acuan
Kejadian adalah suatu peristiwa
fisika yang terjadi dalam suatu ruang pada suatu waktu tertentu. Seseorang yang
mengamati suatu kejadian dan melakukan pengukuran, misalnya pengukuran
koordinat dan waktu, disebut pengamat. Alat ukur apa saja yang melakukan
pengukuran terhadap suatu kejadian juga disebut pengamat.
Untuk
menentukan letak sebuah titik dalam ruang, memerlukan suatu sistem koordinat
atau kerangka acuan. Jadi kerangka acuan adalah suatu sistem koordinat,
misalnya sistem koordinat (x, y, z) di mana seorang pengamat melakukan
pengamatan terhadap suatu kejadian.kerangka acuan juga dapat dinyatakan sebagai
suatu patokan yang dapat digunakan
ilmuawan untuk menganalsis hukum gerak atau tempat suatu pengamat dan pengamat
sendiri dapat memiliki dua kemungkinan yaitu pengamat yang diam dan pengamat
yang bergerak.
Ø Relativitas
Newton
Teori relativitas muncul dari
kebutuhan terhadap kerangka acuan. Benda akan dikatakan bergerak apabila
kedudukan benda tersebut berubah terhadap kerangka acuannya. Kerangka acuan di
mana Hukum Newton berlaku disebut kerangka acuan inersia. Kerangka acuan
inersia adalah kerangka acuan yang didalamnya tidak teramati adanya percepatan
tanpa kehadiran gaya eksternal. Jika memiliki dua kerangka acuan inersia yang
bergerak dengan kecepatan konstan relatif terhadap yang lainnya, maka tidak
dapat ditentukan bagian mana yang diam dan bagian mana yang bergerak atau
keduanya bergerak. Hal ini merupakan konsep Relativitas Newton yang menyatakan “ gerak mutlak tidak dapat
dideteksi ”.
Konsep ini dikenal oleh para
ilmuwan pada abad ke-17. Tetapi pada akhir abad ke-19 pemikiran ini berubah.
Sejak saat itu konsep relativitas Newton tidak berlaku lagi dan gerak mutlak
dideteksi dengan prinsip pengukuran kecepatan cahaya.
Pada
relativitas Newton, semua besaran akan sama saat diukur oleh pengamat yang diam maupun pengamat yang bergerak.
Besaran yang berubah hanyalah kecepatan relatif dan berlaku persamaan berikut.
v’ = v - vx
dengan v’
= kecepatan relatif benda terhadap pengamat bergerak
vx
= kecepatan relatif benda terhadap pengamat diam
v
= kecepatan pengamat bergerak terhadap
pengamat diam
B.
Transformasi
Galileo
Untuk
dapat memindahkan koordinat ruang dan waktu suatu kejadian yang berlangsung di
dalam sebuah kerangka acuan inersia ke dalam kerangka acuan lain yang bergerak
dengan kecepatan relatif yang konstan
dapat dilakukan dengan transformasi
Galileo.
Pada
gambar 1 terdapat dua kerangka acuan inersia S dan S’. S diam dan S’
bergerak dengan kecepatan v terhadap S
sepanjang sumbu X positif. Misalkan S sebagai stasiun dan S’ sebagai kereta api
yang bergerak dengan kecepatan konstan v.
|
|
Gambar 1. kerangka
acuan inersia. S diam dan S bergerak dengan kecepatan v terhadap S.
Mula-mula S dan S’ berimpit lalu
setelah t sekon, S’ sudah menempuh jarak d = vt. Seorang penumpang P di dalam
kereta terhadap kerangka acuan S bergerak dengan kecepatan tetap ux,
searah dengan v. Pada saat t sekon, P mempunyai koordinat P (x, y, z) terhadap kerangka acuan S dan
mempunyai koordinat P (x’, y’, z’ ) terhadap kerangka acuan S’ dengan hubungan
Persamaan ( 1 )
disebut transformasi Galileo
Untuk menentukan
kecepatan, persamaan ( 1 ) diturunkan terhadap waktu t. Dalam transformasi
Galileo, t’ = t, sehingga
 adalah
kecepatan P terhadap S’
adalah
kecepatan P terhadap S’
adalah
kecepatan P terhadap S
dan
,sehingga
ux’
= ux – v
dengan cara yang sama diperoleh uy’ = uy dan uz’ = uz ,
sehingga transformasi Galileo untuk kecepatan adalah
Untuk mendapatkan percepatan, persamaan ( 2 )
diturunkan terhadap waktu. Karena v konstan, maka
sehingga berlaku hubungan
|
|
(3)
C.
POSTULAT
RELATIVIAS KHUSUS
Pada tahun 1888 Hertz berhasil
membuktikan hipotesis Maxwell bahwa
cahaya termasuk gelombang elektromagnetik, yang melalui udara dengan
kecepatan c = 3x108 m/s. Sesuai dengan pendapat umum pada saat itu
bahwa gelombang memerlukan medium untuk merambat, para ilmuawan kemudian
mengemukakan hipotesis eter, “ jagat raya
dipenuhi oleh eter stasioner yang tidak
mempuyai wujud tetapi dapat menghantarkan perambatan gelombang”.
a.
Percobaan
Michelson-Morley
Pada tahun 1887, Albert
A. Michelson (1852-1931) dan Edward
W. Morley (1838-1923) melakukan percobaan untuk mengukur kelajuan bumi
relarif terhadap eter. Kedua fisikawan berkebangsaan Amerika ini membuat
peralatan yang terkenal dengan nama interferometer Michelson (gambar 2), yang
cukup teliti untuk dapat mengukur kelajuan bumi relatif terhadap eter. Satu
lengan interferometer (lengan 1) diarahkan sejajar dengan arah gerak melalui
eter. Kecepatan bumi melalui eter akan sama dengan kecepatan eter melalui bumi dalam arah
berlawanan, dengan kelajuan v, seperti ditunjukan gambar 2.a
|
|

|
|
(a)
(b)
|
v
|
|
c
|
|
v’=c-v
|
|
v
|
|
c
|
|
v’=c+v
|
(c)
|
v’
|
|
c
|
|
v
|
|
v’
|
|
c
|
|
v
|
(d)
Gambar
2 (a) Diagram interferometer Michelson. (b) Analogi gerak cahaya melalui “angin
eter” dengan gerak perahu melalui “arus” sungai. (c) Diagram vektor untuk
perahu bergerak searah dan menentang arah arus air. (d) Diagram vektor untuk
perahu menyeberangi arus air.
c = kecepatan perahu terhadap
arus perahu = cahaya
v’ = kecepatan perahu terhadap
acuan tanah arus = eter
v
= kecepatan arus terhadap acuan tanah tanah
= bumi
Untuk
memudahkan perhitungan, kita dapat melakukan analogi.” Angin eter ” yang memenuhi jagat raya dianalogikan dengan
“arus air” pada sungai, cahaya dianalogikan dengan perahu, dan bumi dianalogikan dengan tanah. Dengan demikian,
kelajuan eter terhadap bumi, v, dianalogikan dengan kelajuan arus terhadap
tanah ( orang yang diam di tepi sungai ). Kelajuan cahaya terhadap eter, c,
dianalogikan dengan kelajuan perahu terhadap arus, dan kelajuan cahaya terhadap
bumi, v’, dianalogikan dengan kelajuan perahu
terhadap tanah. Sesuai dengan definisi penjumlahan vektor kecepatan
relatif , maka
vperahu,arus
= vperahu,tanah + vtanah,arus
c
= v’ + (-v)
Vektor kecepatan perahu terhadap
tanah v’, adalah resultan dari vektor kecepatan perahu terhadap arus dan vektor
kecepatan arus terhadap tanah.
Untuk
gerak perahu (cahaya) searah arus (eter) dari A ke B, dan gerak balik perahu
(cahaya) dari B ke A berlawana arus (gambar 2.c) akan diperoleh
tAB = =
=
dan tBA
=
selang waktu
untuk menempuh lintasan AB pergi-pulang (lambang t//) sama dengan selang waktu untuk menempuh
AB ditambah BA.
t//
= tAB + tBA =
+
=
|
t// =
|
(5)
Untuk
gerak perahu (cahaya) tegak lurus arah
arus (eter) dari A ke C dan balik dari C ke A, v’=
(gambar 2.b)
|
|

(6)
Dari persamaan (5)
dan (6) diperoleh beda waktu antara t// dan
,
(7)
dan
persamaan (7), menjadi
(8)
Kedua berkas cahaya (yang sejajar
maupun tegak lurus) ini mulanya sefase dan ketika keduaya kembali akan dibentuk
pola interferensi karena adanya beda waktu.
Inrterferometer
diatur untuk frige-fringe paralel dan teleskop pengamat difokuskan pada satu
dari frinji-frinji ini (satu frinji adalah jarak antara dua pita terang
berdekatan). Beda waktu di antara kedua berkas cahaya menghasilkan satu
beda fase ketika keduanya bergabung di
posisi teleskop. Satu beda fase pola interferensi akan dideteksi dengan memutar
interferometer melalui sudut 90
dalam bidang horizontal, sedemikan sehingga
kedua berkas bertukar peran. Ini
mengahasilkan beda waktu dua kali dari yang diberikan dalam persamaan. Beda
lintasan berdasarkan beda waktu ini adalah
Pergeseran
frinji
yang berkaitan adalah sama dengan beda lintasan ini dibagi dengan
panjang gelombang cahaya, , karena perubahan dalam lintasan 1 berkaitan dengan
|
Pergeseran =
|
(9)
Dalam
percobaan Michelson dan Morley ini, tiap berkas cahaya dipantulkan oleh cermin
beberapa kali untuk memberikan suatu panjang lintasan efektif L kira-kira 11m. Dengan menggunakan
nilai L ini dan mengambil kelajuan bumi terhadap matahari, v, sama dengan 3 x
104 m/s, diperoleh
Ketelitian
instrumen yang didesain oleh Michelson dan Morley memiliki kemampuan mendeteksi
pergesera dalam pola frinji sekecil 0,01. Tetapi dalam pecobaan ini keduanya
mendeteksi tidak ada pergeseran dalam pola-pola frinji. Sejak itu, percobaan
ini telah diulang beberapa kali oleh berbagai ilmuwan dibawah kondisi yang
berbeda, tetapi tetap tidak ada pergeseran fringe yang pernah diamati. Karena
itu, disimpulkan bahwa tak ada seorangpun yang mendeteksi kecepatan gerak bumi
dengan mengacu pada eter.
b.
Postulat Eistein
Setelah terbukti bahwa eter tidak
dapat dibuktikan keberadaannya Albert
Einstein (1879-1955) pada tahun 1905 mengumumkan teori relativitas khusus, dan sepuluh tahun kemudian mengusulkan teori relativitas umum. Teori
relativitas khusus bertolak dari kerangka acuan inersia, yaitu kerangka acuan
yang bergerak dengan kecepatan tetap terhadap kerangka acuan lainnya;
sedangkan, teori relativitas umum bertolak dari kerangka acuan yang bergerak
dipercepat relatif terhadap kerangka acuan yang lain.
Hasil
percobaan Michelson dan Morley yang telah meletakkan dasar dua postulat
Einstein. Kedua postulat tersebut kemudian menjadi dasar teori relativitas
khusus. Kedua postulat itu adalah;
Postulat pertama,
hukum – hukum memiliki bentuk yang sama
pada semua kerangka acuan inersia.
Postulat kedua,
cahaya merambat melalui ruang hampa dengan
kecepatan tetap c tidak bergantung pada kecepatan sumber atau pengamat. Kecepatan cahaya di
ruang hampa sebesar c = 3. 108
m/s.
Postulat pertama dinyatakan karena
tidak ada kerangka acuan universal sebagai
acuan mutlak. Postulat pertama ini adalah perluasan dari prinsip relativitas
Newton untuk memasukan bukan hanya hukum-hukum mekanika, tetapi juga
hukum-hukum fisika lainnya.
Posulat kedua mempunyai implikasi
yang sangat luas. Hukum penjumlahan kecepatan tidak berlaku untuk cahaya.
Menurut Einstein, waktu t’ tidak sama dengan t sehingga relativitas Newton dan
transformasi Galieo tidak dapat digunakan. Kecepatan, waktu, panjang, dan massa
benda semuanya bersifat relatif.
c.
Transformasi Lorentz
Transformasi Galileo hanya berlaku
jika kecepatan-kecepatan yang digunakan tidak bersifat relativistik, yaitu jauh
lebih kecil daripada kecepatan cahaya c. Untuk peristiwa yang lebih luas hingga
kecepatan yang menyamai kecepatan cahaya, diperlukan suatu transformasi baru
sehingga diperoleh bahwa kecepatan cahaya dalam vakum merupakan besaran mutlak.
Untuk memasukkan konsep relativitas
Einstein, selang waktu menurut kerangka acuan bergerak t tidak sama dengan
selang waktu menurut kerangka acuan bergerak t’. Oleh karena itu, hubungan
transformasi mengandung suatu pengali
, disebut tetapan transformasi. Dengan demikian, jika transformasi ini
dianggap linear, persamaan (1) menjadi
|
x’ =
|
(10)
Jika kerangka acuan O’ terhadap kerangka
acuan O bergerak ke kanan dengan kecepatan tetap v, kerangka acuan S terhadap
S’ dapat dianggap bergerak relatif ke kiri dengan kecepatan v. Hubungan x
terhadap x’ menjadi
|
x =
|

(11)
Substitusi nilai x’ dari persamaan (10)
ke dalam persamaan (11) menghasilkan
x =
=
2
( x – vt ) +
vt’
|
t’ =
|
(12)
Misalkan, kecepatan P terhadap kerangka
acuan O’ pada subbab sebelumnya adalah kecepatan cahaya ux’ = c,
maka menurut Einstein kecepatan cahaya terhadap kerangka acuan O sama besarnya,
yaitu ux = c. Dari sini diperoleh hubungan x = ct dan x’ = ct
sehingga persamaan (10) menjadi ct’ =
(
x – vt ). Kemudian, dengan menggunakan nilai t’dari persamaan (12) diperoleh
c
=
(
x – vt )
Faktor yang mengandung x dikumpulkan di
sebelah kiri, sehingga
x
= ct
x = ct
Karena x = ct,
maka
1
+
=
1
(13)
|
|
(13)
Dengan
mensubtitusikan persamaan (13) diperoleh bentuk persamaan transformasi Lorentz,
yaitu:
|
x’ =
y’ = y
z’ = z
t’ =
|
(14)
Transformasi Lorentz
untuk kecepatan
Kecepatan
dapat diperoleh dari turunan pertama fungsi kedudukan terhadap waktu.
Dari persamaan (14)
diperoleh hasil diferensial,
dx’
=
dan
dt’ =
ux’
=
=
=
|
ux’ =
|
(15)
uy’
=
=
=
=
uz
=
Persamaan (15)
dapat ditulis menjadi
ux’
= ux
v
atau ux’
= ux
v
|
ux
=
|
(16)
Dengan penalaran
yang sama, nilai
|
uy =
|
(17)
Penjumlahan kecepatan berdasarkan relativitas
Einstein
Tinjau
penjumlahan kecepatan dalam satu arah, yaitu arah horizontal sepanjang sumbu X.
Misalkan, suatu kerangka acuan S’ bergerak dengan kecepatan v dalam arah sumbu
X terhadap kerangka acuan S yang diam. Sebuah benda terhadap S’ bergerak dengan
kecepatan ux’ dalam arah sumbu X. Sesuai transformasi Lorentz, kecepatan
benda tersebut terhadap S, yaitu ux, dirumuskan dengan
|
ux
=
|
(18)
d.
Dilatasi waktu
Menurut
Einstein, selang waktu yang terukur oleh pengamat yang diam terhadap kejadian
dan yang terukur oleh pengamat yang bergerak dengan kelajuan konstan terhadap
kejadian tidaklah sama. Hal ini terjadi karena waktu bukanlah suatu besaran mutlak.
Untuk memahami hal tersebut, tinjaulah Gambar 4.
|
C
|
|
S
|
|
C
|
|
y
|
|
x
|
|
r
|
|
v
|
|
B
|
|
A
|
(a) (b)
|
Gambar
lintasan cahaya menurut pengamat yang (a) diam dan (b) bergerak dengan
kelajuan tetap terhadap kejadian untuk membuktikan adanya pemuluran waktu.
|
Seberkas cahaya dipancarkan dari sebuah sumber S menuju sebuah cermin C
yang terpisah pada jarak y. Pengamat yang diam terhadap peristiwa akan
mendapati cahaya datang dan cahaya pantul melalui lintasan yang sama, seperti
diperlihatkan pada gambar 4 (a). Selang waktu yang diperlukan oleh cahaya untuk
menempuh lintasan bolak-balik adalah
Dilain pihak, menurut pengamat yang bergerak dengan kelajuan v terhadap peristiwa
akan mendapati litasan cahaya menjadi seperti yang diperlihatkan pada gambar
4(b). Dalam selang waktu
, sumber cahaya telah menempuh jarak AB,
yakni 2x = v
. Selanjutnya dengan menggunakan dalil
phytagoras diperoleh
r
=
atau r =
selang waktu yang
diperoleh cahaya untuk menempuh
lintasan ACB adalah
|
|
(19)
Dengan
= selang waktu
yang terukur oleh pengamat yang bergerak dengan kelajuan v terhadap kejadian
Persamaan di
atas menunjukkan bahwa
>
karena
Dengan
kata lain, waktu yang terukur oleh pengamat yang bergerak dengan kelajuan v
terhadap kejadian lebih lama (mulur) dari waktu yang terukur oleh pengamat yang
diam terhadaap kejadian. Persamaan di atas di kenal sebagai pemulur waktu.
Waktu yang terukur oleh pengamat yang diam terhadap kejadian (
) disebut waktu benar.
e.
Kontraksi panjang
Selain
selang waktu, panjang sebuah benda juga bersifat relatif, bergantung pada kerangka acuan.
Untuk itu, tinjaulah sebuah pesawat yang bergerak dengan kelajuan v dari A ke
B, seperti pada gambar di bawah ini.
|
v
|
|
A
|
|
B
|
|
L0
|
Jarak
A dan B adalah tetap (L0). Seorang pengamat yang diam relatif
terhadap kedua titik akan mengukur panjang AB sebenarnya, yakni L0. Dilain
pihak, jarak AB menurut pilot (L), adalah
L
= v
Dengan
adalah selang
waktu yang diperlukan pesawat untuk menempuh jarak AB menurut pilot.selang
waktu yang terukur menurut pengamat adalah
. Jadi menurut pengamat, jarak AB adalah
L0
= v
Hubungan
antara L dan L0 dapat ditentukan dengan membandingkan keduanya
sebagai berikut.
dari persamaan
dilatasi diperoleh
Dengan demikian
|
L
= L0
|
(20)
dengan : L =
panjang benda bergerak yang diamati oleh kerangaka acuan yang diam
L0 = panjang benda yang diam pada suatu kerangaka acaun
v = kecepatan benda terhadap kerangka acuan
yang diam
D.
Massa,
momentum, dan energi relativistik
1.
Massa relativistik
Menurut fisika Newton
atau fisika klasik, massa benda konstan tidak bergantung pada kecepatan. Tetapi
berdasarkan teori relativitas Einstein, massa benda adalah besaran relatif.
Massa benda yang bergerak (m) relatif terhadap seorang pengamat akan lebih
besar daripada massa diam (m0) benda tersebut. massa benda yang
bergerak dengan kecepatan v adalah
|
m
=
m =
|
(21)
Perubahan
massa karena gerak benda hanya dapat diabaikan untuk benda yang bergerak dengan
kecepatan yang jauh lebih kecil daripada kecepatan cahaya. Dengan kata lain,
fisika Newton hanya berlaku untuk benda-benda yang kecepatannya jauh lebih
kecil daripada kecepatan cahaya (v
c).
2.
Momentum relativistik
Ketika
kelajuan partikel hampir mendekati kelajuan cahaya, persamaan momentum dan
energi kinetik nonrelativistik tidak bisa berlaku lagi. Dengan mendefinisikan
ulang momentum dan energi kinetik, sehingga hukum kekekalan berlaku pada
kelajuan berapapun. Persamaan nonrelativistik p = mv dan EK =
mv2 benar selama kelajuan v
c. Persamaan
relativitas lebih berlaku umum, karena persamaan ini memberikan nilai
momentum yang benar pada kelajuan berapapun.
Untuk
benda – benda yang bergerak mendekati kecepatan cahaya, momentum
relativistiknya diperoleh dengan memperhatikan massa relativistik benda sesuai
dengan persamaan (21), sehingga diperoleh persamaan
|
p =
p =
|
(22)
3.
Energi relativistik
Dalam
mekanika klasik, usaha yang dilakukan oleh gaya yang bekerja pada partikel sama
dengan perubahan pada energi kinetik partikel tersebut. Sebagaimana dalam mekanika
klasik, kita akan mendefinisikan energi kinetik sebagai kerja yang dilakukan
oleh gaya dalam mempercepat partikel dari keadaan diam hingga mencapai
kecepatan tertentu. Jadi,
Ek
=
=
(23)
dengan
v =
, jadi:
Kemudian,
persamaan tersebut disubstitusikan ke persamaan (), maka diperoleh:
Ek
=
=
atau
Ek
=
(24)
Suku
kedua persamaan () tidak bergantung pada kecepatan dan disebut energi diam
partikel
,
yang merupakan perkalian massa diam dengan c2.
Jumlah
energi kinetik dan energi diam disebut energi relativistik, yaitu
E
= Ek +
=
E
=
(26)